Subspace generative… Subspace Generative Adversarial Learning for Unsupervised Outlier Detection!#
This was the title of my Bachelor’s Thesis. At first glance, it might seem like this is just one big buzzword bingo. However, if we explore the work done, we quickly notice that it actually describes the thesis well… Now, let’s dive right into what I did and why this seemingly buzzy title is not so buzzy afterall.
The Idea#
In recent years, deep generative methods have enabled several subfields of Machine Learning to make great progress. Previously overshadowed by supervised methods, these unsupervised methods now thrive as they yield impressive performance without the need of labels. Particularly, the introduction of Generative Adversarial Networks (GAN) and their game-theoretical approach to Deep Learning proved how powerful generative methods are. GANs manage to generate realistic data, thus they are suited for many different Machine Learning tasks such as Novelty Detection or Image Generation. Especially for high-dimensional data, GANs impress with their performance. Over the years, several extensions to the GAN framework have been published, leveraging the generative nature of the model to detect outliers. While there are models like MO-GAAL, which embed an ensemble structure to GANs to generate outliers, or AnoGAN, which works with a latent representation of data to detect outliers, all of these GAN extensions still lack one property: subspace Search. In high-dimensional spaces, outliers are sometimes only, or better, visible in some feature subspaces, making it hard to find them when only looking at the full set of features.
That is why we want to combine the generative strength of GANs with a feature subspace ensemble to tackle this missed opportunity. To achieve this, we have to solve a few issues:
- Redesign the model architecture
- Redesign the gametheoretical gnerative approach
- Handle feature dependencies
With FeGAN, the model proposed by us, we manage to utilize the generative nature of GANs to learn the distribution of multiple feature subspaces. This allows to look for outliers in these subspaces respectively and therefore achieve a higher success rate in Outlier Detection.
Generative Adversarial Networks#
GANs typically consist of two neural networks: A Generator G and a Discriminator D. Each of those two parties has one unique goal. The generator aims to, almost, approximate the underlying data distribution. Ideally, G is able to generate realistic data samples at the end of the training. Its counterpart, the Discriminator, doesn’t really care about the underlying distribution as much. D’s actual goal is quite simple as it is to distinguish between real data samples and the ones generated by G.
One can imagine the GAN training procedure as a feud between an art forger and an art expert. While the art expert’s job is to be really good at spotting fake art, the art forger tries to trick the expert. During the game, the art forger becomes better and better at faking artwork, while, at some point, the art expert might not be able to distinguish between real and fake artwork anymore.
This training results in a minimax (zero-sum) game, which is held by two parties.
If you’re interested in the deeper maths behind this model or other details, please refer to the original GAN paper.
Feature Ensemble GAN - FeGAN#
The first step to solve our task is to adjust the model architecture and think about how we can incorporate multiple subspaces into the training process. A very naive approach would be to simply use multiple GANs, each training on its own, unique, subspace. However, that doesn’t help us much as each Generator would only be able to generate samples from that subspace. Therefore, we would not approximate the full sample space and probably lose important feature dependencies. So, what do we do now? How about we only use one Generator, that trains on the full feature space? And then we project the generated full dimensional samples down to specific subspaces? That way, we still generate on the complete feature space while also enabling the Discriminators to work on lower-dimensional subspaces. Of course, this is only possible if the Discriminators work with lower-dimensional datasets to begin with.
That second idea is what we chose for FeGAN. We use one Generator working on the full feature space, and let it interact with N Discriminators, each training on their own unique subspace.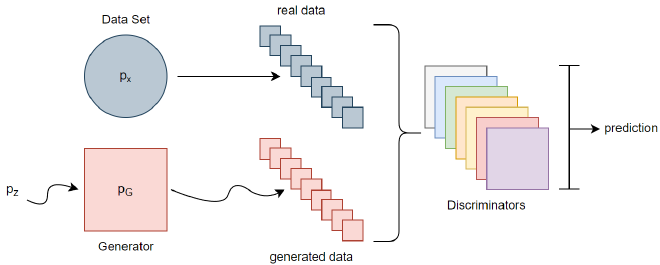
The adjusted architecture already gives a good direction on how the target function and the minimax game of the original GAN have to be adjusted in order to work. However, I choose not to go into detail here, as it is plain math. Since I’ve already written my thesis, you can simple head there and look it up if you are interested (hint: you can also look here)!
Something not so clear is the selection of “good” subspaces. Ideally, we want subspaces to be informative and independent to prevent redundancy. Unfortunately, due to the exponential number of possible subspaces, choosing the “good” ones, is very hard. While there are certain algorithms for this, they all have their pros and cons and we chose to stick to the most simple method: Random selection. Admittedly, this may not be the best choice in terms of prediction accuracy, but it is sufficient to prove the functionality of the model.
Conclusion#
In my thesis, we extended the vanilla GAN architecture to create FeGAN. We combine one Generator with multiple Discriminators, each working on their on unique feature subspace to form one ensemble, improving prediction quality. Furthermore, we adjusted the training process, the zero-sum game and the target function, to make the original GAN training compatible with our novel adjustments.
The code for FeGAN (old name, now rebranded to GSAAL) can be found on my GitHub.
Final words & Future#
We were really satisfied with the results of FeGAN. That’s why we’ve decided to continue researching the model and write a paper about it! At the moment, we are in the reviewing process of a major conference, but a pre-print version is already available on arxiv.
